how to find range of a function algebraically

Polynomial
Degree
Linear office
Slopey-intercept
x-intercept
Root
Zero (of a function)Quadratic function
Quadratic formula Rational role

Objectives

Identify polynomials and their basic characteristics
Ascertain rational functions
Find the domain, range, and roots of unproblematic polynomials and rational functions

Introduction to Polynomials

Polynomials are a type of role that yous will see regularly as yous report mathematics. A polynomial is a series of terms, each of which is the product of a constant coefficient and an integer power of the contained variable. A full general polynomial function f in terms of the variable x is expressed below.

Hither, the coefficients c_i are constant, and n is the degree of the polynomial (n must be an integer where 0 ≤ n < ∞). Note that a line, which has the form (or, perhaps more familiarly, y = mx + b), is a polynomial of degree one--or a offset-degree polynomial. A quadratic role, , is a second-degree polynomial.

Linear Functions

Linear functions (autonomously from constant, or zeroth-caste functions) are the simplest kind of polynomial. Given the class , the slope of the line is c ₁ and the y-intercept is c ₀. Here, the slope is defined equally the alter in the value of f (or Δf) divided by a corresponding change in x (or Δx), and the y-intercept is the value of f at 10 = 0. These characteristics are illustrated graphically beneath for the role .

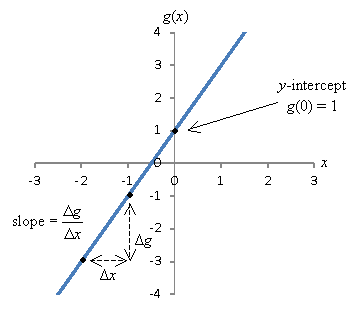
In general, many functions have y-intercepts--again, for a function f(x), this is merely f(0). (Not all functions accept a y-intercept however, as not all are defined at x = 0. For instance, the part is not divers at x = 0, so it has no y-intercept.) Because a role must pass the vertical line test as nosotros noted previously, a function can have at well-nigh i y-intercept.

Some functions may also have x-intercepts: for a function g(x), these are values of ten for which g(x) = 0. In other words, an x-intercept is a solution to the equation g(10) = 0. The values of x that satisfy this equation are likewise chosen roots or zeroes of the function. A part may have many, one, or no roots. In our linear case higher up, the function has a root at , since

The root of this office is illustrated graphically beneath.

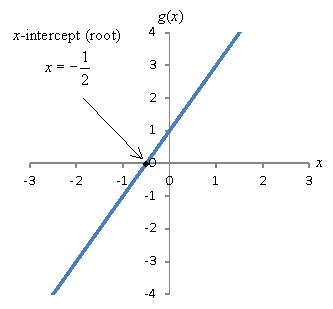
Quadratic Functions

You may too be familiar with quadratic functions (2nd-degree polynomials), which take the course . Quadratic functions, like all polynomials, have a y-intercept c ₀. They can accept none, one, or ii roots, which tin be adamant using the quadratic formula, which is expressed beneath.

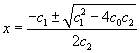
Note that a commencement-degree polynomial (linear function) tin but take a maximum of one root. The pattern holds for all polynomials: a polynomial of root n tin have a maximum of n roots.

Practice Trouble: Find the roots, if they exist, of the function .

Solution: You can use a number of unlike solution methods. One is to evaluate the quadratic formula:

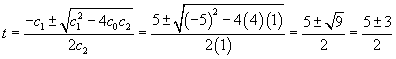
t = 1, 4

Alternatively, y'all can factor to find the values of x that make the part h equal to zero.

t = 1, 4

You lot can as well graph the role to find the location of roots--but exist certain to examination your answers in the equation, as graphs are non exact solution methods by and large. The graph for h(t) is shown below with the roots marked with points.

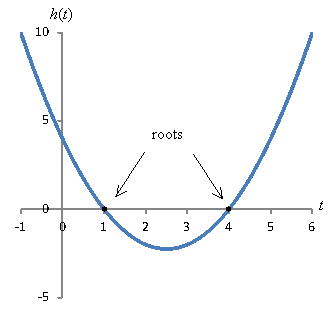
Finding the roots of higher-degree polynomials is a more complicated task.

Introduction to Rational Functions

Rational functions are fractions involving polynomials. A rational function f(10) has the general course shown below, where p(x) and q(x) are polynomials of any degree (with the caveat that q(x) ≠ 0, since that would result in an #ff0000 office).

Note that all polynomials are rational functions (a polynomial is a rational function for which q(10) = ane), but not all rational functions are polynomials. An example of a rational function is the following.

A note of caution: although you can simplify the expression higher up, the outcome may not exist identical to the original function. To illustrate this betoken, permit's factor the numerator of g(r).

Naturally, the temptation is to abolish one factor of r – 1 from both the numerator and the denominator, leaving the expression below:

Thus, we come across that g(r) is linear. And if we graph the first expression (with the polynomial denominator), the event will be the line r – 1 except that r cannot equal 1, since r = ane is non in the domain of m(r). In the graph, this strange result appears equally a "hole," equally illustrated below using an open circle at r = ane. Thus, we must treat rational functions carefully with regard to changing the expression.

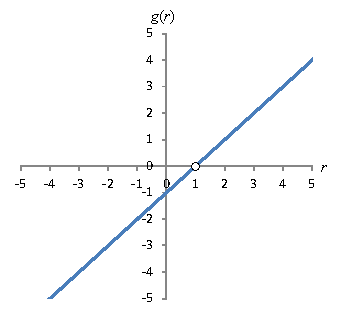
Practise Trouble: Detect the domain and range of the function , and graph the office.

Solution: The domain of a polynomial is the unabridged set of real numbers. The limiting cistron on the domain for a rational function is the denominator, which cannot be equal to goose egg. The values non included in the domain of t(x) are the roots of the polynomial in the denominator. Allow'south gene both the numerator and denominator.

We tin can see from this factoring that the domain of t(x) is all real numbers except 10 = –1. That is, the domain includes the intervals (-∞,-1) and (-i, ∞). To find the range, permit'southward plot the graph of the function. To do and then, we can simplify it by eliminating like factors:

Since the limitation that x cannot exist –1 remains subsequently simplification, we can plot the simplified role without worrying most neglecting holes in the graph.

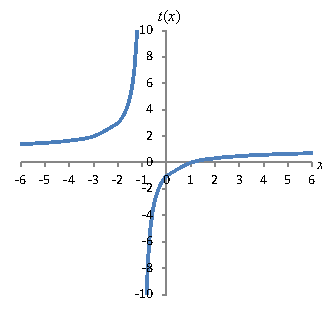
Note that the x can never be –1 because the function goes to infinity (or negative infinity) as it approaches this value. Also note that the range of the office includes all existent values except t = one. It gets very close to t = ane, but it never reaches this value (the numerator is never equal to the denominator!).

Source: https://www.universalclass.com/articles/math/pre-calculus/find-domain-range-roots-polynomials-rational-functions.htm

Posted by: smithelifuldn2000.blogspot.com